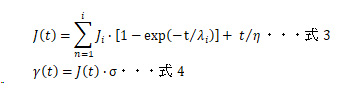業務案内

動的粘弾性 測定事例11

スペクトルを用いた粘弾性予測〜樹脂(高密度ポリエチレンHDPE)の過渡応答予測〜

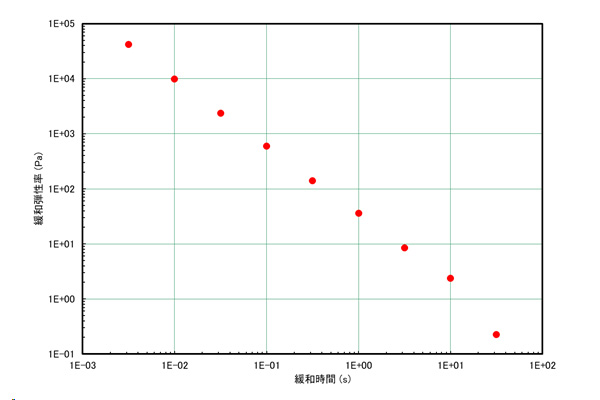
粘弾性の緩和弾性率予測を行うため材料の緩和スペクトルを用意する。
ここでは基準温度160℃におけるHDPEの離散型緩和スペクトルを使用する。作成方法は、測定事例9を参照

一般化マクスウェルモデルで緩和弾性率を表すと式1となる。
（式１中のG(t)は系全体の緩和弾性率、tは時間、τiは各緩和成分の緩和時間、Giは各緩和成分の緩和弾性率である。）
各緩和成分の緩和時間τi、各成分の緩和弾性率Giを代入することで緩和弾性率が求められる。
緩和弾性率G(t)に材料に加えたひずみγを乗ずることで、縦軸を応力σ(t)に変換することが可能である（式2）。
線形ひずみでは、緩和弾性率曲線が変わらないが、非線形ひずみの場合ひずみの増加に伴う弾性率の減衰を考慮する必要がある。

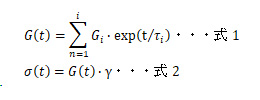
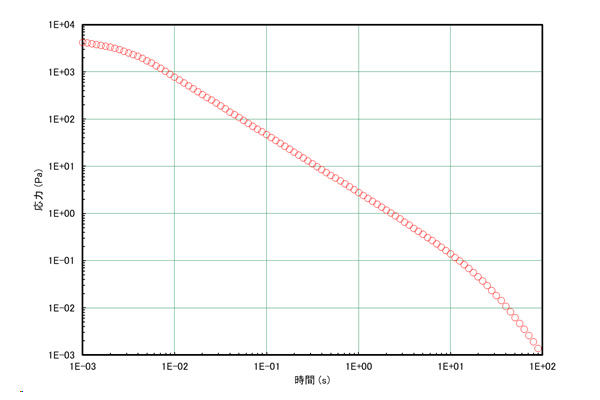
粘弾性のクリープ予測を行うため材料の遅延スペクトルを用意する。
ここでは基準温度160℃におけるHDPEの離散型遅延スペクトルを使用する。作成方法は、測定事例10を参照

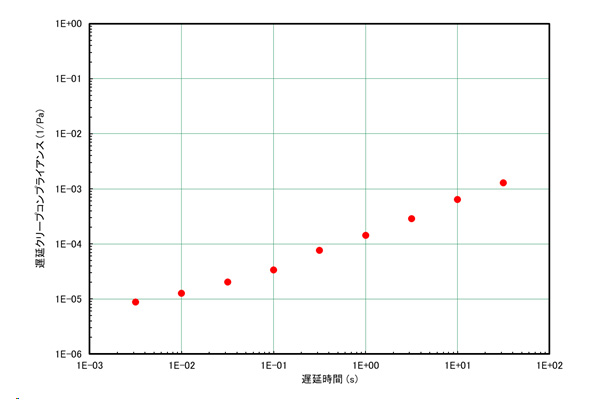
一般化フォークトモデルでクリープを表すと式3となる。
（式3中のJ(t)は系全体の遅延クリープコンプライアンス、tは時間、λiは各遅延成分の遅延時間、Jiは各遅延成分の遅延クリープコンプライアンスである。）
各成分の遅延時間λi、各成分の遅延クリープコンプライアンスJiを代入することで遅延クリープコンプライアンスJ(t)が求められる。
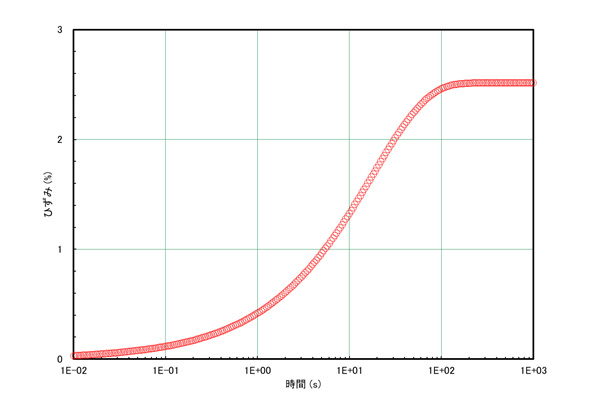
遅延クリープコンプライアンスJ(t)に材料に加わえた応力σを乗ずることで、縦軸をひずみγ(t)に変換することが可能である(式4)。
線形応力であれば遅延クリープコンプライアンスJ(t)の曲線は変わらないが、非線形応力の場合応力の増加に伴うクリープコンプライアンスの上昇を考慮する必要がある。

←測定事例10測定事例1→

レオロジーTOPページへ