業務案内
- Home
- 業務案内
- 材料・成分の総合評価(ゴム・プラスチック等)
- レオロジー・粘弾性
- 周波数依存性測定
粘弾性
周波数依存性測定
周波数依存性測定は、材料固有の特性を評価できます。弾性と粘性は、材料の種類、変形の周波数(速度)等によって変化します。内部構造の推定ができ、分子量及び分子量分布の評価、充填材の分散性等の相対評価も可能です。
図1は、一般的な材料の貯蔵弾性率及び損失弾性率の周波数依存性の概略図です。図中の貯蔵弾性率及び損失弾性率は、4つの温度領域に分類され、温度依存性のグラフを左右反転させたようなグラフとなります。横軸の周波数は、Hzもしくはrad/sで表記します(1 Hz = 2πrad/s)。固体を測定する分野ではHzが用いられ、液体・溶融体を測定する分野ではrad/sが用いられます。Cox-merz則CoxとMerzが発見した周波数を振って測定した粘度と一定速度で流した粘度が一致するという法則。なぜ一致するかは現在も不明が成り立つ場合、周波数rad/sとひずみ速度1/sを同等として取り扱えます。ただし比較する際には、rad/sの単位で比較する必要があります。
それぞれ①ガラス領域、②ガラス転移領域、③ゴム領域、④流動領域に対応します。
①~③は、DMA測定装置(RSA-G2、DMA+1000)で測定します。
③~④は、回転レオメータ(ARES-G2、RPA2000)で測定します。
周波数依存性において、測定する材料は、印加した周波数によって異なるスケールの内部の構造が振動します。(動的粘弾性と振り子を参照)
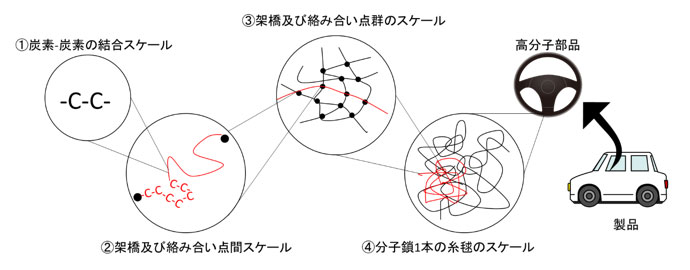
内部の構造は、次の①~④のスケール
①では炭素-炭素の結合スケール
②では架橋及び絡み合い点間のスケール
③では架橋及び絡み合い点群のスケール
④では分子鎖1本の糸毬のスケール
がそれぞれ対応し、その運動特性から内部構造の存在量を定性評価できます。
固体微粒子を添加した材料では、④において貯蔵弾性率が一定の値になる範囲(第二平坦部)が現れるため、凝集構造の評価に使われます。凝集が系全体に広がれば第二平坦部が広くなり、分散性が上がれば狭くなります(図2)。
また④の領域は、測定対象の一番大きな要素に対応しており、最長緩和時間(すべての要素が緩和した状態)及びゼロせん断粘度(せん断速度に依存しない粘度)を評価できます。
③の貯蔵弾性率の高さは、架橋及び絡み合い点の密度を反映しており、貯蔵弾性率が一定の値になる範囲(ゴム平坦部)の広さは材料の分子量を反映しています。
③から④にかけての損失弾性率のピークの広がりは分子量分布を反映しており、分子量分布が広い場合にはブロードになります。
①及び②における貯蔵弾性率及び損失弾性率は、分子鎖の主鎖骨格に左右されます。
周波数依存性測定は、温度依存性測定とは違い、材料固有の特性となります。ただしひずみは、線形ひずみであることを事前にひずみ依存性測定で確認することが必須であり、分解等を起こす材料は時間依存性測定(周波数一定)で測定時間中に材料に変化がないことを確認することが必須です。
-
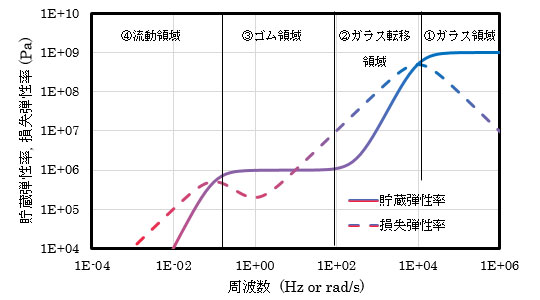
- 図1 一般的な非晶性材料の周波数依存性測定結果の概略図
-
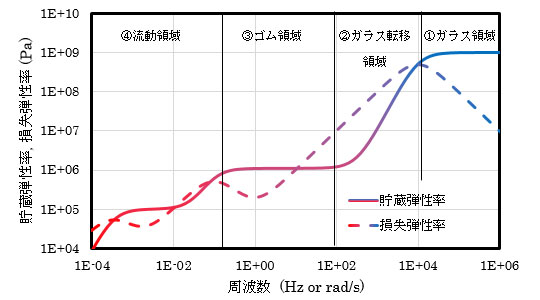
- 図2 固体微粒子を添加した材料の周波数依存性測定結果の概略図